by Dr. David Stewart
by Dr. David Stewart
The Chemistry of Essential Oils [1]
What is Proof?
Absolute proof is strictly the domain of logicians. In mathematics, for example, once a theorem is proven it is proven for all time and all circumstances. Mathematical proof is absolute. Mathematics, however, is not science. This is a point about which many are confused. Mathematics is a language used by science, but is not itself a science. Mathematical proof and scientific proof are not the same thing at all.
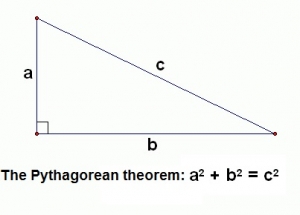
To see this point more clearly, consider the Pythagorean Theorem—a mathematical proof that relates the lengths of the sides (a & b) of a right triangle to the length of its hypotenuse (c). (See the figure above.)
This theorem was proven thousands of years ago once and for all time. We needn’t worry that tomorrow a right triangle may be discovered that disproves the theorem. Neither should we be concerned that the theorem was proven in Greece and, therefore, may or may not apply to the United States or to astronauts on another planet. Proof of the Pythagorean Theorem is absolute—valid for all times and places. In mathematics, once proven is always proven. This is not so in science.
The reason that mathematicians can prove their theorems absolutely is because their universe of mathematics is a creation of human consciousness. The elements of this universe (numbers, functions, vectors, etc.) were all conceived and defined by mathematicians themselves. Therefore, since they created their own universe and, in principle, have knowledge of all of its parts, when they prove a theorem they are assured that the proof will stand for all time and in all places, because in making the proof they were able to consider their entire universe whose complete past, present, and future they know.
To think of it another way, mathematics, as are all systems of logic, is similar to a game with certain elements and rules devised by somebody in an arbitrary, but definite and orderly fashion. Once the game is established, the elements and the rules are not changed. If you change anything, you have a different game. When you prove a mathematical theorem you are merely playing the game as defined by the system of mathematics in which you are engaged. By agreement with other mathematicians, you must make your proof using only the elements and rules laid down for the particular mathematical system in which you are working. If you change the rules then you are not playing the game—you are inventing a new game or a new system of mathematics with different conditions.
Take baseball, for example. The elements of the game are the ball, the bat, the bases, the field, and the players. Among the established rules is that three outs constitute the end of a team’s time up to bat for that inning. Now this is a completely arbitrary rule. It could have been decided that two outs would do it, or five, or seven, but for some reason, three was chosen. If we want to make it something different, then we cannot call it baseball. In any case, once the game begins, the rules remain fixed. In a mathematical sense, you could prove that if one member of your team strikes out, another pops a fly to shortstop, and a third is thrown out on first, your team is finished batting for that inning. This proof would be absolute because it is based upon a finite set of elements and rules that were invented by man. Even if afterwards someone changes the rules and elements so that three outs no longer retires the side up to bat, they will have only changed the game to something else. They will not have affected the absoluteness of your former proof since now, in effect, they are talking about a different game than the one in which you made your proof.
Just as there are many kinds of games, there are many systems of mathematics. In Euclidian Geometry the shortest distance between two points is a straight line. This follows from the manner in which the elements and rules of Euclidian Geometry are defined. In some other systems of geometry the shortest distance between two points is not a straight line. This does not disprove the Euclidian notion any more than citing the case of bowling, where the high score wins, can be used to disprove that the low score wins in golf. The two systems of geometry are entirely different games. All they have in common is that both were fashioned by the human mind.
Mathematics as Evidence of God’s Image in Man
While we have compared various systems of mathematics with various games, this is not to put mathematics in the same category as games. Games are truly arbitrary—products of the whims of their creators and subject to changes by those who play the games over time. Mathematics is different. It is not arbitrary and certain fundamentals are not subject to change in time, which is the real reason mathematical proofs stand forever without fear of disproof.
The superficial aspects of mathematics are arbitrary. For example, the choices of how mathematical concepts are represented are arbitrary since these are made by humans. This includes choices such as how to represent the number one—whether in Arabic symbols, Roman numerals, Chinese characters, or the hieroglyphics of ancient Egypt. But the concept of “one” is not an arbitrary, man-made choice. It is a fixed principle of God’s universe and remains unchanged regardless of the symbol by which is represented.
Mathematician and physicist, Dr. Edward Close, has pointed out that there is an uncanny correlation between mathematical systems and the observed universe, which gives physics and chemistry their quantitative basis. Close said:
“I think that, as a creation of the human mind, mathematics may well be one of the best indications that man is, indeed, made in God’s image, since this human creation mimics God’s creation—the observable universe—so well. The truth is, that no logical/mathematical system can ever be complete within itself, but must be an expression of something beyond itself. This innate feature of all mathematical systems is the thrust of Godel’s Incompleteness Theorem.”
In other words, if God’s infinite consciousness is one of form, structure, and order, then we, as living creations made in his image (as stated in Genesis 1:26-27) would reflect a parallel form, structure, and order in our individualized consciousness. Furthermore, if the projection of God’s consciousness as individualized human consciousness reflects his attributes of form, structure, and order, then all the rest of his creation (as stated in Romans 1:20) would also reflect a parallel form, structure, and order. Thus, when humans create logical systems of form, structure, and order from their own minds (such as a system of mathematics), it is not surprising that such mental constructs would find a close correlation with physical reality, as found in the quantitative sciences.
In Close’s book, Transcendental Physics, he states this concept as follows:
“If primary consciousness (God) has form and structure, it should be reflected, at least partially, in individual consciousness, and in the structure of the physical universe. If all structure is projected from primary consciousness, we can understand why logical structure, thought to originate in human minds, is repeatedly found to apply to the structure of the physical universe. The human mind and the physical universe display the same symmetry and logic because that symmetry and logic underlie all reality in the substance of primary consciousness (God).”
Thus, while mathematical systems, and logical systems of all kinds, are creations of the human mind, they are not as arbitrary as the whimsical creation of games. There is an unseen universal archetype that guides and validates the precepts of mathematics. As stated at the outset of this discussion on “What is Proof?”— Absolute proof is strictly the domain of logicians.
Mathematical proof and scientific proof are not the same thing at all.
What is Scientific Proof?
Scientific proof is not really proof at all, in the mathematical sense, but is either verification or disproof. Since scientists deal with a universe that is not of their own creation, they cannot prove their laws absolutely as can mathematicians. Although scientists use the term “scientific proof,” and I may use it in this book, what we really mean is that a particular hypothesis has been verified or disproved. We don’t mean “proof” in the mathematical sense.
Scientists can never know for a certainty that the laws seemingly in effect today were always so or that they will be in effect at all future times. Neither can they know that their laws, as observed to date, within the limits of current observations, will continue to be upheld by future observations. That is to say, just because Newton’s laws have been repeatedly verified during the last two centuries doesn’t mean they functioned, as we observe them today, at all times in the geologic past or during the days of creation when God spoke the universe into existence.
Is the Speed of Light a Constant?
Consider the speed of light in a vacuum—186,280 miles per second or 300,000 km/sec. Twentieth-century physicists consider it to be an invariable constant of the universe. But is it? Do we really know that the speed of light was the same five-thousand or five-million years ago? Will it remain constant for all time into the future?
Some scientists, such as Barry Setterfield (A Brief History of c – 1987), say the speed of light used to be much faster and is gradually slowing down. Einstein’s famous equation, E = mc2, can be used to deduce this conclusion. Solving for c (the speed of light), we find that it equals the square-root of the energy of the universe (E) over the mass (m).
If we assume that no additional energy (E) or mass (m) is being fed into the physical universe and if our observations and conclusions about the ongoing transformation of energy into mass throughout the universe is correct, then the amount of total energy in the universe (E) is continually diminishing while the total mass (m) is increasing causing the ratio E/m to get smaller and smaller in time, thus causing the speed of light to also gradually get slower and slower over the centuries. Of course, we made a few assumptions in drawing this conclusion which may turn out to be invalid. Even so, it does illustrate a point, that things we consider constant and factual today may not always have been so.
Science Cannot Directly Observe the Past
Science can only directly observe the present. We can extrapolate into the future and deduce conclusions about the past, but only the present is directly within the grasp of scientific observation. Geologists deduce that dinosaurs once thundered across the earth’s surface, but no scientist has ever seen one alive. What we know of them we can only deduce from their remains.
Science is Limited by Space
Science is also limited in its contact with space. The universe in which we live is limitless in two opposing directions—expansively outward into the farthest reaches of unplumbed space and infinitesimally inward into the subspace of the atoms. Since absolute proof in the physical universe would require knowledge of every cubic centimeter of matter, space and energy, and since humans have no such knowledge of their universe (as mathematicians do of theirs)—absolute proofs of physical phenomena are impossible for human scientists.
If you think about it, comprehension of every speck of matter and every corner of space in the created universe is tantamount to the definitions for “omnipresence” and “omniscience”—neither of which are human attributes. In most religions, however, these are attributes of the divine. What this implies is that if you seek absolute answers about the manifested universe, they cannot be found by materialistic science. A quest for absolute truth always leads beyond science and leads into matters which are spiritual and inaccessible to our logical left brains.
The point is that scientists can never know all the elements and rules of their universe because not only did they not create it, at least a portion of it will always remain beyond them in time and/or space—where the term “space” is used here to designate the limitlessness of both the inner and the outer universes.
Unlike mathematics, the tenets of science are forever in jeopardy of ambush by a new set of facts. How many ideas formerly considered scientifically sound are now considered disproven? How many times has medical science reversed itself? How much of present-day medical practice, deemed scientific and beneficial today, will, in a few years, be demonstrated unscientific and harmful? For all we know, science may eventually invalidate them all.
Bleeding patients with leeches as a routine medical cure-all procedure sounds absurd to us now, but during the nineteenth century it was considered good medical practice. Within the framework of the scientific understanding of the time, it seemed most reasonable.
Scientific laws describe only what we see here and now within the limits of our history and of our restricted vision. Science, at best, can only provide us with a set of likely probabilities based upon and limited by current data. No matter how much data has been accumulated on growing basil or lavender over decades, or even centuries, we will never be able to predict the exact chemical composition of the next batch of essential oil harvested for a given field or from any field.
Some sciences can offer more certainty than others. Physics and chemistry are among the more certain sciences.
Medical and biological science, by contrast, are among those whose probabilities are among the least certain because of the unimaginable complexity of life processes, their unknown interactions with the human mind and spirit, and the impossibility of objective and complete measurement.
For more on this topic see: The Limitations of Science and the Medical Paradigm [2]
Excerpted from the book: The Chemistry of Essential Oils Made Simple: God’s Love Manifest in Molecules [1] – pages 618 – 654
Reprinted with permission from the author and publisher.
Copyright Care Publications – All rights reserved.
About the Author
Dr. David Stewart studied theology, philosophy, and English at Central Methodist College in Fayette, Missouri (1955-58) and studied chemistry, biology and social sciences at Central Missouri State University in Warrensburg (1962-63). He also studied commercial photography at Los Angeles Trade Technical College (1959-60). He completed a BS degree in Mathematics and Physics at Missouri School of Mines and Metallurgy in 1965 and was salutatorian of his graduating class. His MS and PhD degrees are in geophysics (theoretical seismology) and were earned from the University of Missouri at Rolla in 1969 and 1971 respectively. He spent a semester in medical school at the University of North Carolina (1973) and has been a Certified Childbirth Educator (CCE) with the American Academy of Husband-Coached Childbirth (AAHCC) since 1975.
Dr. Stewart is also a Registered Aromatherapist (RA) with the nationally recognized Aromatherapy Registration Council (ARC), which is endorsed by the National Association of Holistic Aromatherapists (NAHA), of which he is a member.
He has held positions as a hydraulic engineer and hydrologist with the U.S. Geological Survey in Southern California (1965-67). He was a professor on the faculty of the University of North Carolina, Chapel Hill, (1971-1978) and also held a professorship at Southeast Missouri State University (1988-1993). He was also a part-time United Methodist Pastor (1993-94, 1997-99) in rural Missouri. He has been the Executive Director of the InterNational Association of Parents and Professionals for Safe Alternatives in Childbirth (NAPSAC International) since its founding in 1975.
For most of his professional career, Dr. Stewart has been self-employed as an author and lecturer, mainly in the area of alternative health care. He has also served on advisory committees to the American Public Health Association (APHA) and the American College of Nurse-Midwives (ACNM). He has testified as an expert on health matters before state legislative committees, U.S. congressional committees, medical licensing boards and courts of law throughout the U.S. as well as in Canada.
He has authored or coauthored over 200 published works including more than a dozen books (including Healing Oils of the Bible [3]). Two of his books won the “Books of the Year” Award from the American Journal of Nursing. One of his flyers on breastfeeding (published by La Leche League International, LLLI) sold over two million copies in ten languages.
See Also: